Hukum De Morgan

Dalam logika proposional dan aljabar Boolean, Hukum De Morgan^[1]^[2]^[3], aturan De Morgan, atau teorema De Morgan^[4] adalah sepasang aturan penarikan kesimpulan yang menghubungkan konjungsi dan disjungsi melalui negasi. Aturan ini dinamai dari Augustus De Morgan, seorang matematikawan abad ke-19 berkebangsaan Inggris.

Hukum De Morgan dapat dinyatakan dalam bahasa Indonesia sebagai:

Negasi dari disjungsi adalah konjungsi dari negasi
Negasi dari konjungsi adalah disjungsi dari negasi

atau

Komplemen dari gabungan dua himpunan sama dengan irisan dari komplemen kedua himpunan tersebut
Komplemen dari irisan dua himpunan sama dengan gabungan dari komplemen kedua himpunan tersebut

atau

bukan ( $A$ atau $B$ ) = (bukan $A$ ) dan (bukan $B$ )
bukan ( $A$ dan $B$ ) = (bukan $A$ ) atau (bukan $B$ )

dengan " $A$ atau $B$ " menyatakan disjungsi inklusif (yang berarti setidaknya satu dari dari $A$ atau $B$ bernilai benar), dan bukan logika disjungsi eksklusif (yang berarti tepat satu dari dari $A$ atau $B$ bernilai benar).

Dalam teori himpunan dan aljabar Boolean, Hukum De Morgan dapat ditulis secara formal sebagai

{\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}}{\text{, dan}}\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}}\end{aligned}}

dengan

$A$ dan $B$ adalah sembarang himpunan
${\overline {A}}$ menyatakan komplemen dari himpunan $A$
$\cap$ menyatakan operasi irisan pada himpunan
$\cup$ menyatakan operasi gabungan pada himpunan

{\displaystyle \neg \phi \lor \neg \psi } — Pembuktian bahwa $\neg \phi \lor \neg \psi$ ekuivalen dengan $\neg \!\left(\phi \land \psi \right)$ menggunakan tabel kebenaran.^[5]

Dalam bahasa formal, Hukum De Morgan dapat ditulis secara formal sebagai

{\begin{aligned}\neg \!\left(P\lor Q\right)&\iff \left(\neg P\right)\land \left(\neg Q\right){\text{, dan}}\\\neg \!\left(P\land Q\right)&\iff \left(\neg P\right)\lor \left(\neg Q\right)\end{aligned}}

dengan

$P$ dan $Q$ merupakan proposisi
$\neg$ menyatakan operator logika negasi (tidak)
$\land$ menyatakan operator logika konjungsi (dan)
$\lor$ menyatakan operator logika disjungsi (atau)
$\iff$ adalah simbol metalogika yang berarti "dalam bukti logis, dapat diganti dengan" dan seringkali dibaca sebagai "jika dan hanya jika". Untuk setiap kombinasi nilai benar/salah untuk $P$ dan $Q$ , ruas kiri dan kanan dari panahnya akan memiliki nilai kebenaran yang sama setelah diselesaikan.

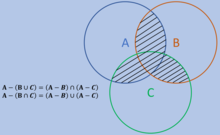
Bentuk lain dari Hukum De Morgan dapat dinyatakan sebagai berikut

{\begin{aligned}A\setminus \left(B\cup C\right)&=\left(A\setminus B\right)\cap \left(A\setminus C\right){\text{, dan}}\\A\setminus \left(B\cap C\right)&=\left(A\setminus B\right)\cup \left(A\setminus C\right)\end{aligned}}

Penerapan dari aturan ini salah satunya ialah menyederhanakan ekspresi logika pada program komputer dan desain rangkaian digital. Hukum De Morgan adalah contoh dari suatu konsep umum dari dualitas matematika.

Notasi Formal

Dengan menggunakan notasi sekuensi, maka aturan negasi dari konjungsi dapat ditulis sebagai berikut :

{\begin{aligned}\neg \!\left(P\land Q\right)&\vdash \left(\neg P\lor \neg Q\right){\text{, dan}}\\\left(\neg P\lor \neg Q\right)&\vdash \neg \!\left(P\land Q\right)\end{aligned}}

Dengan cara serupa, aturan negasi dari disjungsi dapat ditulis dalam notasi sekuensi sebagai berikut :

{\begin{aligned}\neg \!\left(P\lor Q\right)&\vdash \left(\neg P\land \neg Q\right){\text{, dan}}\\\left(\neg P\lor \neg Q\right)&\vdash \neg \!\left(P\land Q\right)\end{aligned}}

Dalam bentuk aturan, negasi dari konjungsi dapat ditulis sebagai berikut :

{\begin{array}{rl}&\neg \!\left(P\land Q\right)\\\hline \therefore &\neg P\lor \neg Q\end{array}}

{\phantom {Spasi}}

{\begin{array}{rl}&\neg P\lor \neg Q\\\hline \therefore &\neg \!\left(P\land Q\right)\end{array}}

Dengan cara serupa, negasi dari konjungsi dapat ditulis sebagai berikut :

{\begin{array}{rl}&\neg \!\left(P\lor Q\right)\\\hline \therefore &\neg P\land \neg Q\end{array}}

{\phantom {Spasi}}

{\begin{array}{rl}&\neg P\land \neg Q\\\hline \therefore &\neg \!\left(P\lor Q\right)\end{array}}

dan saat dituliskan sebagai suatu teorema dalam logika proposisional, maka Hukum De Morgan dapat dinyatakan sebagai

{\begin{aligned}\neg \!\left(P\lor Q\right)&\leftrightarrow \left(\neg P\right)\land \left(\neg Q\right){\text{, dan}}\\\neg \!\left(P\land Q\right)&\leftrightarrow \left(\neg P\right)\lor \left(\neg Q\right)\end{aligned}}

dengan

P

dan

Q

adalah proposisi yang diekspresikan dalam suatu sistem formal. Hukum De Morgan yang diperumum menawarkan ekuivalensi saat menegasikan konjungsi atau disjungsi yang melibatkan banyak suku. Jika

P_{k}

menyatakan proposisi ke-

k

, maka Hukum De Morgan yang diperumum ialah

{\begin{aligned}\neg \!\left(P_{1}\lor P_{2}\lor \ldots \lor P_{n}\right)&\leftrightarrow \neg P_{1}\land \neg P_{2}\land \ldots \land \neg P_{n}{\text{, dan}}\\\neg \!\left(P_{1}\land P_{2}\land \ldots \land P_{n}\right)&\leftrightarrow \neg P_{1}\lor \neg P_{2}\lor \ldots \lor \neg P_{n}\end{aligned}}

Teori himpunan

Dalam teori himpunan, Hukum De Morgan seringkali dinyatakan sebagai "gabungan dan irisan ditukar saat dikomplemenkan",^[6] yang dapat dinyatakan secara formal sebagai berikut :

{\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}}{\text{, dan}}\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}}\end{aligned}}

dengan

$A$ dan $B$ adalah sembarang himpunan
${\overline {A}}$ menyatakan komplemen dari himpunan $A$
$\cap$ menyatakan operasi irisan pada himpunan
$\cup$ menyatakan operasi gabungan pada himpunan

Hukum De Morgan juga dapat diperumum untuk sembarang jumlah himpunan, yaitu

{\begin{aligned}{\overline {\bigcup _{i\,\in \,I}A_{i}}}&=\bigcap _{i\,\in \,I}{\overline {A_{i}}}{\text{, dan}}\\{\overline {\bigcap _{i\,\in \,I}A_{i}}}&=\bigcup _{i\,\in \,I}{\overline {A_{i}}}\end{aligned}}

dengan

I

adalah suatu himpunan indeks (bisa himpunan terhitung, maupun himpunan tak terhitung)

Rekayasa

Dalam aljabar Boolean, teknik listrik dan teknik komputer, Hukum De Morgan biasa ditulis sebagai berikut :

{\begin{aligned}{\overline {A+B}}&={\overline {A}}\cdot {\overline {B}}{\text{, dan}}\\{\overline {A\cdot B}}&={\overline {A}}+{\overline {B}}\end{aligned}}

dengan

${\overline {A}}$ menyatakan operator logika negasi (TIDAK) dari $A$
$\cdot$ menyatakan operator logika konjungsi (DAN)
$+$ menyatakan operator logika disjungsi (ATAU)

Pencarian teks

Hukum De Morgan sering digunakan dalam pencarian teks menggunakan operator Boolean DAN, ATAU, dan BUKAN (TIDAK). Misalkan terdapat beberapa dokumen yang memuat kata "merah" dan "biru". Hukum De Morgan menyatakan bahwa kedua pencarian ini akan menghasilkan dokumen-dokumen yang sama :

Pencarian A : BUKAN (merah ATAU biru)

Pencarian B : (BUKAN merah) DAN (BUKAN biru)

Dokumen-dokumen yang memuat kata "Merah" atau "biru" dapat dikelompokkan menjadi empat kategori, yaitu :

Kategori 1 : Hanya memuat kata "merah"

Kategori 2 : Hanya memuat kata "biru"

Kategori 3 : Memuat kata "merah" dan juga "biru"

Kategori 4 : Tidak memuat kata "merah" maupun "biru"

Di satu sisi, jelas bahwa pencarian "(merah ATAU biru)" akan menampilkan kategori 1, 2, dan 3. Akibatnya, negasi dari pencarian tersebut (yaitu hasil pencarian A) akan menampilkan dokumen-dokumen lainnya, yaitu dokumen-dokumen pada kategori 4.

Di sisi lain, pencarian "(BUKAN merah)" akan menampilkan kategori 2 dan kategori 4, dan pencarian "(BUKAN biru)" akan menampilkan kategori 1 dan kategori 4. Dengan menerapkan operator DAN pada kedua pencarian ini (yaitu pencarian B), maka hasilnya akan menampilkan hasil yang sama-sama dijumpai pada kedua pencarian ini, yaitu dokumen-dokumen pada kategori 4.

Argumentasi serupa juga dapat diterapkan pada dua pencarian berikut

Pencarian C : BUKAN (merah DAN biru)

Pencarian D : (BUKAN merah) ATAU (BUKAN biru)

yang sama-sama menampilkan dokumen-dokumen pada kategori 1, 2, dan 4

Bukti formal

Disini, akan digunakan notasi ${\overline {A}}$ untuk menyatakan komplemen dari himpunan $A$ , sama seperti penggunaan pada § Teori himpunan. Untuk membuktikan bahwa ${\overline {A\cup B}}={\overline {A}}\cap {\overline {B}}$ , maka

Bagian pertama

Akan dibuktikan bahwa ${\overline {A\cup B}}\subseteq {\overline {A}}\cap {\overline {B}}$ . Diambil sembarang elemen $x\in {\overline {A\cup B}}$ . Perhatikan bahwa

{\begin{aligned}x\in {\overline {A\cup B}}&\implies x\not \in A\cup B&{\text{definisi operasi komplemen}}\\&\implies x\not \in A\;\land \;x\not \in B&{\text{lihat penjelasan dibawah}}\\&\implies x\in {\overline {A}}\;\land \;x\in {\overline {B}}&{\text{definisi operasi komplemen}}\\&\implies x\in {\overline {A}}\cap {\overline {B}}&{\text{definisi operasi irisan}}\end{aligned}}

Penjelasan baris kedua
Akan dibuktikan bahwa $x\not \in A\cup B$ akan mengakibatkan $x\not \in A$ dan $x\not \in B$ melalui kontradiksi. Andaikan $x\in A$ , maka $x\in A\cup B$ . Akan tetapi, hal itu mustahil terjadi, sebab diperoleh informasi bahwasanya $x\not \in A\cup B$ pada baris pertama di atas. Oleh karena terjadi kontradiksi, maka pengandaian di awal (bahwasanya $x\in A$ ) bernilai salah. Akibatnya, diperoleh $x\not \in A$ . Andaikan $x\in B$ , maka $x\in A\cup B$ . Akan tetapi, hal itu mustahil terjadi, sebab diperoleh informasi bahwasanya $x\not \in A\cup B$ pada baris pertama di atas. Oleh karena terjadi kontradiksi, maka pengandaian di awal (bahwasanya $x\in B$ ) bernilai salah. Akibatnya, diperoleh $x\not \in B$ . Dari dua kasus di atas, maka terbukti bahwa $x\not \in A\cup B$ akan mengakibatkan $x\not \in A$ dan $x\not \in B$ .

Penjelasan baris kedua

Akan dibuktikan bahwa $x\not \in A\cup B$ akan mengakibatkan $x\not \in A$ dan $x\not \in B$ melalui kontradiksi.

Andaikan $x\in A$ , maka $x\in A\cup B$ . Akan tetapi, hal itu mustahil terjadi, sebab diperoleh informasi bahwasanya $x\not \in A\cup B$ pada baris pertama di atas. Oleh karena terjadi kontradiksi, maka pengandaian di awal (bahwasanya $x\in A$ ) bernilai salah. Akibatnya, diperoleh $x\not \in A$ .
Andaikan $x\in B$ , maka $x\in A\cup B$ . Akan tetapi, hal itu mustahil terjadi, sebab diperoleh informasi bahwasanya $x\not \in A\cup B$ pada baris pertama di atas. Oleh karena terjadi kontradiksi, maka pengandaian di awal (bahwasanya $x\in B$ ) bernilai salah. Akibatnya, diperoleh $x\not \in B$ .

Dari dua kasus di atas, maka terbukti bahwa $x\not \in A\cup B$ akan mengakibatkan $x\not \in A$ dan $x\not \in B$ .

sehingga terbukti bahwa ${\overline {A\cup B}}\subseteq {\overline {A}}\cap {\overline {B}}$ .

Bagian kedua

Akan dibuktikan bahwa ${\overline {A}}\cap {\overline {B}}\subseteq {\overline {A\cup B}}$ . Diambil sembarang elemen $x\in {\overline {A}}\cap {\overline {B}}$ . Perhatikan bahwa

{\begin{aligned}x\in {\overline {A}}\cap {\overline {B}}&\implies x\in {\overline {A}}\;\land \;x\in {\overline {B}}&{\text{definisi operasi irisan}}\\&\implies x\not \in A\;\land \;x\not \in B&{\text{definisi operasi komplemen}}\\&\implies x\not \in A\cup B&{\text{lihat penjelasan di}}\\&\implies x\in {\overline {A\cup B}}&{\text{definisi operasi komplemen}}\end{aligned}}

Penjelasan baris ketiga
Akan dibuktikan bahwa $x\not \in A$ dan $x\not \in B$ akan mengakibatkan $x\not \in A\cup B$ melalui kontradiksi. Andaikan $x\in A\cup B$ , maka menurut definisi operasi gabungan pada himpunan, diperoleh $x\in A$ atau $x\in B$ . Jika $x\in A$ , maka hal tersebut kontradiksi dengan hasil pada baris kedua di atas (bahwasanya $x\not \in A$ ) Jika $x\in B$ , maka hal tersebut kontradiksi dengan hasil pada baris kedua di atas (bahwasanya $x\not \in B$ ) Oleh karena terjadi kontradiksi pada kedua kasus di atas, maka pengandaian di awal (bahwasanya $x\in A\cup B$ ) bernilai salah. Akibatnya, terbukti bahwa informasi $x\not \in A$ dan $x\not \in B$ akan mengakibatkan $x\not \in A\cup B$ .

Penjelasan baris ketiga

Akan dibuktikan bahwa $x\not \in A$ dan $x\not \in B$ akan mengakibatkan $x\not \in A\cup B$ melalui kontradiksi. Andaikan $x\in A\cup B$ , maka menurut definisi operasi gabungan pada himpunan, diperoleh $x\in A$ atau $x\in B$ .

Jika $x\in A$ , maka hal tersebut kontradiksi dengan hasil pada baris kedua di atas (bahwasanya $x\not \in A$ )
Jika $x\in B$ , maka hal tersebut kontradiksi dengan hasil pada baris kedua di atas (bahwasanya $x\not \in B$ )

Oleh karena terjadi kontradiksi pada kedua kasus di atas, maka pengandaian di awal (bahwasanya $x\in A\cup B$ ) bernilai salah. Akibatnya, terbukti bahwa informasi $x\not \in A$ dan $x\not \in B$ akan mengakibatkan $x\not \in A\cup B$ .

sehingga terbukti bahwa ${\overline {A}}\cap {\overline {B}}\subseteq {\overline {A\cup B}}$ .

Argumentasi serupa juga dapat digunakan untuk membuktikan bahwa ${\overline {A\cap B}}={\overline {A}}\cup {\overline {B}}$

Referensi

^ Copi, Irving M.; Cohen, Carl; McMahon, Kenneth (2016). Introduction to Logic [Pengantar Logika] (dalam bahasa Inggris). doi:10.4324/9781315510897. ISBN 9781315510880.
^ Hurley, Patrick J. (2015), A Concise Introduction to Logic [Pengantar Singkat mengenai Logika] (dalam bahasa Inggris) (edisi ke-12th), Cengage Learning, ISBN 978-1-285-19654-1
^ Moore, Brooke Noel (2012). Critical thinking [Berpikir Kritis] (dalam bahasa Inggris). Richard Parker (edisi ke-10th). New York: McGraw-Hill. ISBN 978-0-07-803828-0. OCLC 689858599.
^ Teorema De Morgan
^ Kashef, Arman. (2023), In Quest of Univeral Logic: A brief overview of formal logic's evolution (dalam bahasa Inggris), doi:10.13140/RG.2.2.24043.82724/1
^ Boolean Algebra by R. L. Goodstein. ISBN 0-486-45894-6

Pranala luar

Hazewinkel, Michiel, ed. (2001) [1994], "Duality principle", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
(Inggris) Weisstein, Eric W. "de Morgan's Laws". MathWorld.
de Morgan's laws di PlanetMath.
Dualitas dalam Logika dan Bahasa, Internet Encyclopedia of Philosophy.

Templat:Logika klasik

Teori himpunan

Umum

Himpunan (matematika)

Aksioma

Adjungsi
Batas ukuran
Determinasi
Gabungan
Himpunan kuasa
Keberaturan
Kebisadibangunan (V=L)
Perluasan
Pasangan
Pemilihan
- tercacah
- terikat
- global
Takhingga
Aksioma Martin

Skema aksioma
- penggantian
- spesifikasi

Operasi

Gabungan
Gabungan lepas
Himpunan kuasa
Hukum De Morgan
Irisan
Komplemen
Produk Kartesius
Selisih himpunan
Beda setangkup

Konsep
Metode

Argumen diagonal
Bilangan kardinal (besar)
Bilangan ordinal
Diagram Venn
Elemen
- pasangan terurut
- rangkap
Hipotesis kontinum
Induksi lintas-hingga
Kardinalitas
Kelas
Keluarga
Korespondensi satu-ke-satu
Pemaksaan
Semesta yang bisa dibangun

Jenis himpunan

Himpunan bagian · Superhimpunan
Berhingga (turun-temurun)
Takhingga (takhingga Dedekind)
Kabur
Kosong
Rekursif
Semesta
Tercacah
Tak tercacah
Transitif

Teori

Aksiomatik
Alternatif
Naif
Teorema Cantor

Zermelo
- Umum
Principia Mathematica
- New Foundations (NF, NFU)
Zermelo–Fraenkel (ZFC)
- von Neumann–Bernays–Gödel (NBG)
  - Morse–Kelley
- Kripke–Platek
- Tarski–Grothendieck